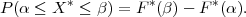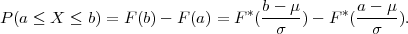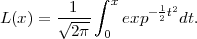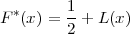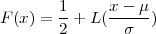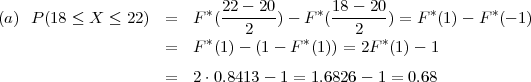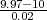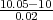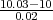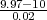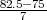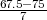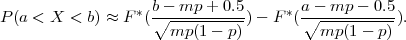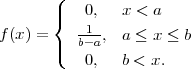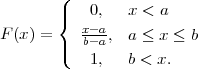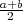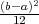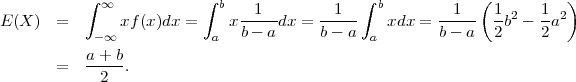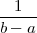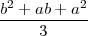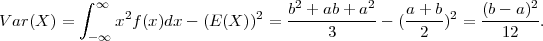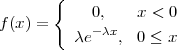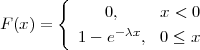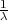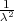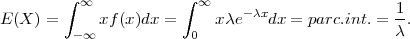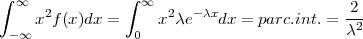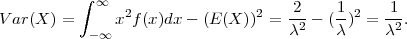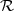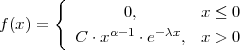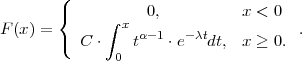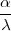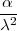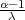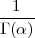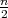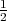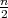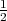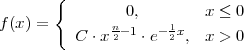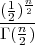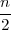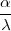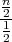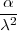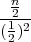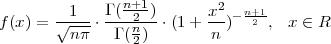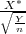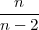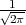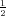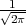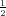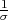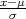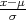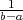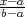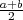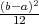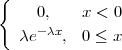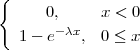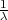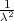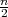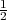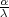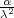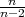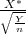Poglavlje 8
PRIMJERI KONTINUIRANIH SLUČAJNIH VARIJABLI
U ovom
poglavlju istaknut ćemo kontinuirane slučajne varijable koje se pojavljuju u odredenim
”scenarijima” i njihove funkcije gustoće vjerojatnosti definirat će se kao specifične
distribucije (razdiobe): normalna, uniformna, eksponencijalna, gama, hi-kvadrat,
Studentova. Normalna distribucija, hi-kvadrat i studentova distribucija imaju veliku
ulogu u matematičkoj statistici.
MOTIV 8.1 Potrošnja materijala u nekom proizvodnom procesu je slučajan
pokus. U prosjeku svaki dan se potroši 20 komada. Svaki mjesec se nabavlja 640
komada potrošnog materijala. Neka je X slučajna varijabla = vrijeme potrebno da
se potroši zaliha (dogodi dogadaj α puta).
(a) Kolika je vjerojatnost da ponestane potrošnog materijal?
(b) Kolika mora biti mjesečna nabavka da vjerojatnost nestašice bude 0.01?
8.1 NORMALNA DISTRIBUCIJA
Najvažnija kontinuirana distibucija je normalna distribucija. Ona se pojavljuje kao
aproksimacija mnogih drugih distribucija i pojavljuje se u mnogim statističkim
testovima.
MOTIV 8.2 Neka je kritična čvrstoća jednog tipa plastičnih ploča normalna
slučajna varijabla X s očekivanom čvrstoćom 1250 kg i standardnom devijacijom
55 kg. Koje je maksimalno opterćenje takvo da je očekivani broj slomljenih ploča
najviše 5%?
Definicija 8.1 (NORMALNA DISTRIBUCIJA)
Za kontinuiranu slučajnu varijablu X* : Ω → ℝ kažemo da ima standardnu
normalnu distribuciju ili standardnu Gaussovu distribuciju s parametrima 0 i 1 i
označavamo X*~ N(0,1) ako ima funkciju gustoće vjerojatnosti
Za kontinuiranu slučajnu varijablu X : Ω → ℝ kažemo da ima normalnu distribuciju ili
Gaussovu distribuciju s parametrima μ i σ i označavamo
X ~ N(μ,σ2) ako ima funkciju gustoće vjerojatnosti
NAPOMENA 8.1 Ako X* ~ N(0,1) ima standardnu normalnu distribuciju,
onda funkcija slučajne varijable X = σ ⋅ X* + μ ima normalnu distribuciju
X ~ N(μ,σ2).
PRIMJER 8.1 Funkcija f*(x) = 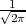 ⋅ e-
⋅ e-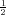 x2 je funkcija gustoće vjerojatnosti.
x2 je funkcija gustoće vjerojatnosti.
Rješenje: Koristimo izvod ∫
-∞∞e-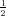 x2
dx =
x2
dx = 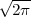 .
.
PRIMJER 8.2 Funkcija distribucije standardne normalne slučajne varijable
X*~ N(0,1) je
Funkcija distribucije normalne slučajne varijable X ~ N(μ,σ2) je
Rješenje: Koristimo definiciju funkcije distribucije kontinuirane slučajne varijable
F*(x) = ∫
-∞xf*(t)dt i formulu za funkciju distribucije za funkciju slučajne varijable
X = σ ⋅ X* + μ, F(y) = F*(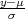 ).
).
PRIMJER 8.3 (a) Za X*~ N(0,1), E(X*) = 0, V ar(X) = 1.
(b) Za X ~ N(μ,σ2), E(X*) = μ, V ar(X) = σ2.
Rješenje: Koristimo izvod ∫
-∞∞x2 ⋅ e-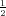 x2
dx =
x2
dx = 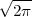 .
.
(a) E(X*) = ∫
-∞∞xf*(x)dx = ∫
-∞∞x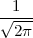 ⋅ e-
⋅ e-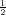 x2
dx = 0 (neparna funkcija).
x2
dx = 0 (neparna funkcija).
(b)
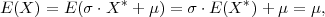
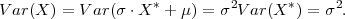
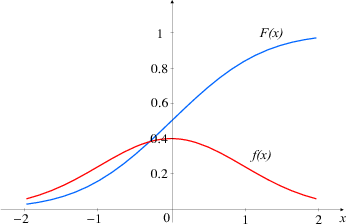
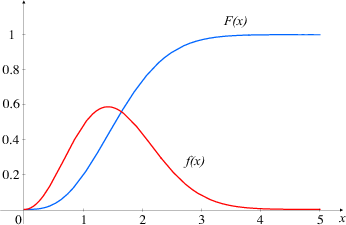
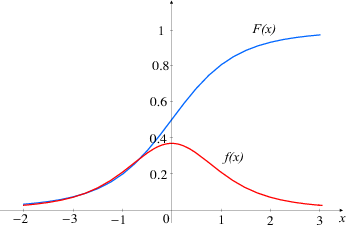
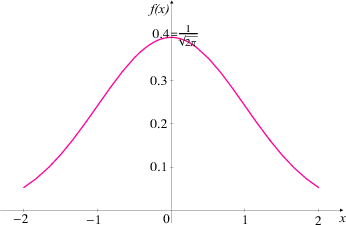
PRIMJER 8.4 Skicirajte graf funkcije gustoće vjerojatnosti f(x). Krivulja se
zove Gaussova zvonolika krivulja. Krivulja je simetrična u odnosu na pravac x = μ.
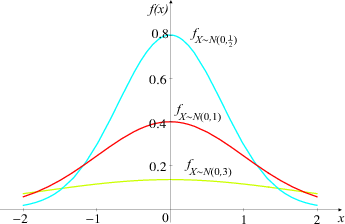
dostiže maksimum u točki (μ,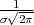 ), a točke infleksije su u μ - σ i μ + σ. Os x
je horizontalna asimptota. Ako σ < 1 graf se sužava i maksimala vrijednost raste,
a ako je σ > 1 graf se širi i maksimalna vrijednost pada.
), a točke infleksije su u μ - σ i μ + σ. Os x
je horizontalna asimptota. Ako σ < 1 graf se sužava i maksimala vrijednost raste,
a ako je σ > 1 graf se širi i maksimalna vrijednost pada.
PRIMJER 8.5 Neka je X*~ N(0,1). Tada možemo izračunati vjerojatnost da
slučajna varijabla X* poprimi vrijednost iz nekog intervala [a,b]:
Neka je X ~ N(μ,σ2). Tada možemo izračunati vjerojatnost da slučajna varijabla
X = σ ⋅ X* + μ poprimi vrijednost iz nekog intervala [a,b]:
NAPOMENA 8.2 U literaturi je poznata Laplaceova funkcija
Ona je obično tabelirana. Veza funkcija F*, F i L(x) je sljedeća:
PRIMJER 8.6 Slučajna varijabla X ~ N(20,4). Provjerite
(a) P(18 ≤ X ≤ 22) = 0.68
(b) P(16 ≤ X ≤ 24) = 0.95
(c) P(14 ≤ X ≤ 26) = 0.99
Rješenje:
PRIMJER 8.7 Slučajna varijabla X ~ N(μ,σ2). Provjerite pravilo 3σ :
(a) P(μ - σ ≤ X ≤ μ + σ) = 0.68
(b) P(μ - 2σ ≤ X ≤ μ + 2σ) = 0.95
(c) P(μ - 3σ ≤ X ≤ μ + 3σ) = 0.99
PRIMJER 8.8
Debljina željeznih ploča ja slučajna varijabla. Možemo pretpostaviti da je to
kontinuirana slučajna varijabla koja ima normalnu distribuciju s očekivanjem
10mm i standardnom devijacijom 0.02mm. Kolika je vjerojatnost defektne ploče
ako je kontrola dala kriterij:
(a) ploča tanja od 9.97 mm,
(b) ploča deblja od 10.05 mm,
(c) ploča odstupa 0.03 mm od 10 mm. U kojim granicama treba biti debljina da bi
u očekivani postotak defektnih ploča bio 5%?
Rješenje:
Za slučajnu varijablu X ~ N(10,0.022) računamo:
(a) P(X < 9.97) = F*(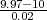 ) = F*(-1.5) = 0.0668. Uz ovaj kriterij očekuje se 6.7%
oštećenih ploča.
) = F*(-1.5) = 0.0668. Uz ovaj kriterij očekuje se 6.7%
oštećenih ploča.
(b) P(X > 10.05) = 1 -F*(10.05) = 1 -F*(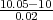 ) = 1 -F*(2.5) = 1 - 0.9938 = 0.0062.
) = 1 -F*(2.5) = 1 - 0.9938 = 0.0062.
Uz ovaj kriterij očekuje se 0.6% oštećenih ploča.
(c) P(9.97 < X < 10.03) = F*(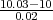 ) -F*(
) -F*(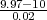 ) = F*(1.5) -F*(-1.5) = 0.8664.
) = F*(1.5) -F*(-1.5) = 0.8664.
1 - P(9.97 < X < 10.03) = 0.1336
Uz ovaj kriterij očekuje se 13.3% oštećenih ploča.
Prema pravilu 3σ :
P(μ - 2σ ≤ X ≤ μ + 2σ) = 0.95,
P(10 - 2 ⋅ 0.02 ≤ X ≤ 10 + 2 ⋅ 0.02) = 0.95.
Uz ovaj kriterij očekuje se 5% oštećenih ploča.
Za 2σ = 0.04 imamo interval dobrih ploča [9.96,10.04].
PRIMJER 8.9 motiv
Neka je kritična čvrstoća jednog tipa plastičnih ploča normalna slučajna
varijabla X s očekivanom čvrstoćom 1250 kg i standardnom devijacijom 55 kg.
Koje je maksimalno opterćenje takvo da je očekivani broj slomljenih ploča najviše
5%?
Rješenje:
Za slučajnu varijablu X ~ N(1250,552) računamo prema pravilu 3σ :
P(μ - 2σ ≤ X ≤ μ + 2σ) = 0.95,
P(1250 - 2 ⋅ 55 ≤ X ≤ 1250 + 2 ⋅ 55) = 0.95. Za maksimalno opterećenje od 1360 kg
očekuje se 5% slomljenih ploča.
PRIMJER 8.10 Na prvoj godini GF studira 200 studenata. Očekivana težina
je 75 kg a standardna devijacija 7 kg. Pretpostavimo da je težina normalno
distribuirana. Koliko studenata ima težinu izmedu 68 kg i 82 kg (tj. zaokruženo od
67.5.5 kg do 82.5 kg)?
Rješenje:
Za slučajnu varijablu težina studenata X ~ N(75,72) računamo:
P(67.5 ≤ X ≤ 82.5) = F*(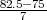 ) -F*(
) -F*(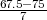 ) = 2F*(1.07) - 1 = 2 ⋅ 0.8577 - 1 = 0.715.
) = 2F*(1.07) - 1 = 2 ⋅ 0.8577 - 1 = 0.715.
Ukupno studenata koji imaju težinu izmedu 68 kg i 82 kg (tj. zaokruženo od 67.5.5 kg
do 82.5 kg) je 200 ⋅ 0.715 = 143.
NAPOMENA 8.3 U graničnom slučaju za velike m binomna distribucija
X ~ B(m,p) se može aproksimirati standardnom normalnom distribucijom. Prema
integralnom Moivre-Laplaceov teoremu (centralni granični teorem za binomnu sl. var.) u
poglavlju 11 vrijedi
Primijetimo da su dodani pribrojnici 0.5 i -0.5 zbog korekcije.
8.2 UNIFORMNA DISTRIBUCIJA
Definicija 8.2 (UNIFORMNA DISTRIBUCIJA)
Za kontinuiranu slučajnu varijablu X : Ω → ℝ kažemo da ima uniformnu
distribuciju na se segmentu [a,b], ako je slika R(X) = R, a funkcija gustoće
vjerojatnosti je
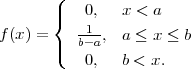
i označavamo X ~ U(a,b).
PRIMJER 8.11 Funkcija distribucije uniformne slučajne varijable X ~ U(a,b)
je
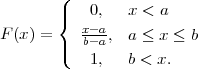
PRIMJER 8.12 Za X ~ U(a,b), E(X) = 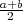 , V ar(X) =
, V ar(X) = 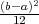 .
.
Rješenje:
∫
-∞∞x2f(x)dx = ∫
abx2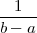 dx =
dx = 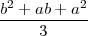
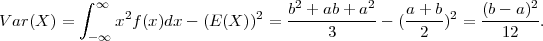
PRIMJER 8.13 Skiciraj graf funkcije gustoće vjerojatnosti i graf funkcije
distribucije vjerojatnosti.
Funkcija f(x) ima prekid u točkama a i b, a funkcija F(x) je neprekinuta na ℝ.
8.3 EKSPONENCIJALNA DISTRIBUCIJA
Eksponencijalna distribucija se pojavljuje u problemima teorije opsluživanja.
MOTIV 8.3 Vrijeme trajanja sijalica je slučajna varijabla X. Uzimamo uzorak
i 5% sijalica traje do 100 sati. Kolika je vjerojatnost da će nova sijalica trajati
duže od 200 sati tj. P(X > 200)?
Definicija 8.3 (EKSPONENCIJALNA DISTRIBUCIJA)
Za kontinuiranu slučajnu varijablu X : Ω → ℝ kažemo da ima eksponencijalnu
distribuciju s parametrom λ, ako je slika R(X) = R, a funkcija gustoće
vjerojatnosti je
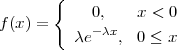
i označavamo X ~ Exp(λ).
PRIMJER 8.14 Funkcija distribucije eksponencijalne slučajne varijable
X ~ Exp(λ) je
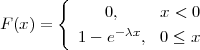
PRIMJER 8.15 Za X ~ Exp(λ), E(X) = 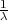 , V ar(X) =
, V ar(X) = 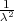 .
.
Rješenje:
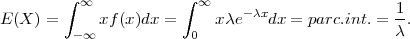
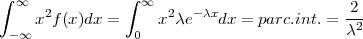
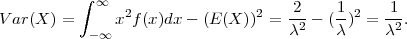
PRIMJER 8.16 Skiciraj graf funkcije gustoće i funkcija distribucije
eksponencijalne slučajne varijable X ~ Exp(λ).
Funkcija f(x) je padajuća funkcija na [0,∞), prekinuta u nuli. Funkcija distribucije
je neprekinuta funkcija R, rastuća, konkavna, ima horizontalnu asimptotu y = 1.
PRIMJER 8.17 motiv
Vrijeme trajanja sijalica je slučajna varijabla koja ima eksponencijalnu
distribuciju s parametrom λ. Uzimamo uzorak i 5% sijalica traje do 100 sati.
(a) Odredite parametar λ.
(b) Kolika je vjerojatnost da će nova sijalica trajati duže od 200 sati?
Rješenje:
(a) X ~ Exp(λ), P(X < 100) = 0.05 ⇒ F(100) = 0.05
F(x) = 1 - e-λx, 0 ≤ x, ⇒ 1 - e-λ⋅100 = 0.05
e-λ⋅100 = 0.95 ⇒ λ ⋅ 100 ≈ 0.051 ⇒ λ ≈ 0.00051.
(b)P(X > 200) | = | 1 - P(X < 200) = e-λ⋅200 ≈ (e-λ⋅100)2 |
| = | (0.95)2 = 0.9025. |
8.4 GAMA DISTRIBUCIJA
Definicija 8.4 (GAMA DISTRIBUCIJA)
Gama distribucija je generalizacija eksponencijalne distribucije.
Neka je slučajni pokus ponavljanje dogadaja u vremenu s zadanim konstantnim
intezitetom (λ). Slučajna varijabla koja daje vrijeme potrebno da se dogadaj dogodi
odredeni broj puta (α) ima gama distibuciju s parametrima α i λ.
Definicija 8.5 (GAMA DISTRIBUCIJA)
Za kontinuiranu slučajnu varijablu X : Ω → ℝ kažemo da ima gama
distribuciju s parametrima α i λ, (α i λ > 0) , ako je slika 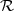 (X) = ℝ, a funkcija
gustoće vjerojatnosti je
(X) = ℝ, a funkcija
gustoće vjerojatnosti je
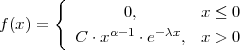
gdje je C = 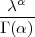 , a Γ(x) = ∫
0∞tx-1 ⋅ e-tdt, Gama funkcija, x > 0 i
označavamo X ~ Γ(α,λ).
, a Γ(x) = ∫
0∞tx-1 ⋅ e-tdt, Gama funkcija, x > 0 i
označavamo X ~ Γ(α,λ).
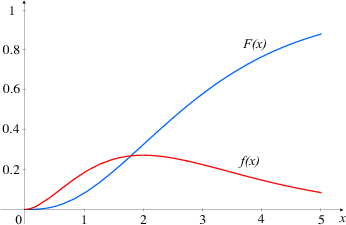
PRIMJER 8.18 Funkcija distribucije gama distribucije X ~ Γ(α,λ) je
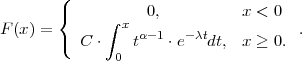
PRIMJER 8.19 SVOJSTVA gama funkcije:
(a) Γ(α + 1) = α ⋅ Γ(α),
(b) Γ(1) = ∫
0∞e-tdt = 1,
(c) Γ(n + 1) = n ⋅ Γ(n) = n ⋅ (n - 1) ⋅ Γ(n - 2) = ... = n!, n ∈ N,
PRIMJER 8.20 Za X ~ Γ(α,λ), E(X) = 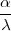 , V ar(X) =
, V ar(X) = 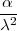 .
.
PRIMJER 8.21 Za α > 1 funkcije gustoće gama distribucije ima maksimum
u x = 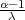 , ima zvonoliki oblik i os x je horizontalna asimptota, a za α < 1,
f(x) je strogo padajuća, konkavna funkcija koja ima vertikalnu asimptotu os y, a
horizontalnu os x.
, ima zvonoliki oblik i os x je horizontalna asimptota, a za α < 1,
f(x) je strogo padajuća, konkavna funkcija koja ima vertikalnu asimptotu os y, a
horizontalnu os x.
Definicija 8.6 (NEPOTPUNA GAMA FUNKCIJA)
Tabelirana je nepotpuna gama funkcija γ(z,α) = 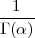 ∫
0ztα-1 ⋅ e-tdt.
∫
0ztα-1 ⋅ e-tdt.
Veza je F(x;α,λ) = γ(λx,α).
PRIMJER 8.22 motiv
Potrošnja materijala u nekom proizvodnom procesu je slučajan pokus. U
prosjeku svaki dan se potroši 20 komada. Svaki mjesec se nabavlja 640 komada
potrošnog materijala. Neka je X slučajna varijabla = vrijeme potrebno da se potroši
zaliha (dogodi dogadaj α puta).
(a) Kolika je vjerojatnost da ponestane potrošnog materijal?
(b) Kolika mora biti mjesečna nabavka da vjerojatnost nestašice bude 0.01?
λ = 20, α = 640, X ~ Γ(α,λ) = Γ(640,20).
Rješenje:
Potrebni podaci: λ = 20, α = 640, X ~ Γ(α,λ) = Γ(640,20).
(a) P(X < 30) = F(30) = F(30;640,20), F(x;α,λ) = γ(λx,α)
F(30;640,20) = γ(20 ⋅ 30,640) = γ(600,640) = 0.057.
Vjerojatnost da bude nestašica je 0.057.
(b) P(X < 30) = 0.01, F(30;α,20) = 0.01
F(30;α,20) = γ(20 ⋅ 30,α) = γ(600,α) = 0.01 ⇒ α = 660.
Potrebne mjesečne zalihe potrošnog materijala su 660 komada da bi
vjerojatnost nestašice bila 0.01 (mala).
PRIMJER 8.23 Za α = 1, gama distribucija je eksponencijalna distribucija
X ~ Γ(1,λ) = Exp(λ).
8.5 HI KVADRAT DISTRIBUCIJA
PRIMJER 8.24 Tabelira se χ2(n), za n = 1,2,...,30, ali u obliku:
za X ~ χ2(n) i zadanu vjerojatnost p = P(X > xp) u tabeli možemo očitati
vrijednosti xp.
Najčešće su tražene vrijednosti za xp, ako su zadane vjerojatnosti p = 0.99,
p = 0.95, p = 0.5, p = 0.1, p = 0.05
PRIMJER 8.25 Neka je X ~ χ2(20) i P(X > xp) = 0.1. Od koje će vrijednosti
slučajna varijabla poprimi veću vrijednost s vjerojatnošću 0.05?
U tablici očitamo za n = 20, i p = 0.1, xp = 28.41.
NAPOMENA 8.4 Neka su slučajne varijable X1,X2,...,Xn takve da sve imaju
standardnu normalnu distribuciju, Xi*~ N(0,1), i = 1,...,n.
Tada slučajna varijabla Y = ∑
i=1n(X
i)2 ima hi kvadrat distribuciju, Y ~ χ2(n).
PRIMJER 8.26 Za X ~ χ2(n), E(X) = n, V ar(X) = 2n.
Rješenje:
Koristimo formulu za očekivanje i varijancu gama distribucije s parametrima
α = 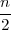 , λ =
, λ =  : E(X) =
: E(X) = 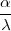 =
= 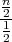 = n, V ar(X) =
= n, V ar(X) = 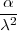 =
= 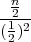 = 2n.
= 2n.
NAPOMENA 8.5 Za X ~ χ2(n) i n →∞, X ~ N(n,2n).
Za X ~ χ2(n) i n > 30, dobra aproksimacija je X ~ N(n,2n).
8.6 STUDENTOVA DISTRIBUCIJA
U matematičkoj statistici važna je Studentova distribucija koju je 1908 definirao S.
Gosset pod pseudonimom Student.
Definicija 8.8 (STUDENTOVA DISTRIBUCIJA)
Za kontinuiranu slučajnu varijablu X : Ω → ℝ kažemo da ima Studentovu
distribuciju ili t -distribuciju s parametrom n (stupanj slobode) i označavamo
X ~ t(n) ako ima funkciju gustoće vjerojatnosti
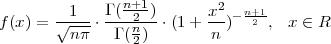
PRIMJER 8.27 Skicirati graf funkcije gustoće vjerojatnosti f(x). Funkcija je
pozitivna, simetrična u odnosu na os y, parna, dostiže maksimum u x = 0, os x je
horizontalna asimptota. Kad n →∞, graf postaje Gaussova krivulja.
PRIMJER 8.28 Tabelira se t(n), za n = 1,2,...,30, ali u obliku:
za X ~ t(n) i zadanu vjerojatnost p = P(|X| > xp) u tabeli možemo očitati
vrijednosti xp.
Najčešće su tražene vrijednosti za xp, ako su zadane vjerojatnosti p = 0.9,
p = 0.8, p = 0.7,..., p = 0.1.
PRIMJER 8.29 Neka je X ~ t(20) i P(|X| > xp) = 0.1. Izvan kojih granica
slučajna varijabla poprimi vrijednost s vjerojatnošću 0.1?
U tablici očitamo za n = 20, i p = 0.1 xp = 1.725.
PRIMJER 8.30 Neka su slučajne varijable X* ~ N(0,1) i Y ~ χ2(n). Tada
slučajna varijabla T = 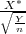 ima Studentovu distribuciju, T ~ t(n).
ima Studentovu distribuciju, T ~ t(n).
NAPOMENA 8.6 Za X ~ t(n), E(X) = 0, V ar(X) = 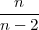 , n > 2.
, n > 2.
NAPOMENA 8.7 Za X ~ t(n) i n →∞, X ~ N(0,1).
Za X ~ t(n) i n > 30, dobra aproksimacija je X ~ N(0,1).
NAPOMENA 8.8 Za n = 1, Studentova distribucija je Cauchyjeva distribucija.
8.7 Ponovimo
STANDARDNA NORMALNA DISTRIBUCIJA (RAZDIOBA)
|
|
| standardna normalna distribucija | X*~ N(0,1) |
|
|
| funkcija gustoće vjerojatnosti | f*(x) = 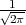 ⋅ e- ⋅ e-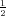 x2 x2 |
|
|
| funkcija distribucije vjerojatnosti | F*(x) = 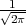 ∫
-∞xe- ∫
-∞xe-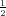 t2dt. t2dt. |
|
|
| očekivanje | E(X) = 0 |
|
|
| varijanca | V ar(X) = 1 |
|
|
| |
NORMALNA DISTRIBUCIJA
|
|
| normalna distribucija | X ~ N(μ,σ2) |
|
|
| funkcija gustoće vjerojatnosti | f(x) = 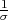 ⋅ f*( ⋅ f*(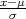 ) ) |
|
|
| funkcija distribucije vjerojatnosti | F(x) = F*(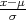 ) ) |
|
|
| očekivanje | E(X) = μ |
|
|
| varijanca | V ar(X) = σ2 |
|
|
| PRAVILO 3σ | za X ~ N(μ,σ) |
|
|
| | P(μ - σ ≤ X ≤ μ + σ) = 0.68 |
|
|
| | P(μ - 2σ ≤ X ≤ μ + 2σ) = 0.95 |
|
|
| | P(μ - 3σ ≤ X ≤ μ + 3σ) = 0.99 |
|
|
| |
UNIFORMNA DISTRIBUCIJA
|
|
| uniformna distribucija | X ~ U(a,b) |
|
|
| funkcija gustoće vjerojatnosti | f(x) = 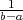 , za a ≤ x ≤ b, , za a ≤ x ≤ b, |
|
|
| funkcija distribucije vjerojatnosti | F(x) = 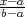 , za a ≤ x ≤ b, , za a ≤ x ≤ b, |
|
|
| očekivanje | E(X) = 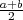 |
|
|
| varijanca | V ar(X) = 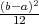 |
|
|
| |
EKSPONENCIJALNA DISTRIBUCIJA
|
|
| eksponencijaln distribucija | X ~ Exp(λ) |
|
|
| funkcija gustoće vjerojatnosti | f(x) = 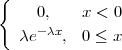 |
|
|
| funkcija distribucije vjerojatnosti | F(x) == 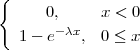 |
|
|
| očekivanje | E(X) = 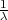 |
|
|
| varijanca | V ar(X) = 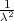 |
|
|
| |
GAMA DISTRIBUCIJA, HI-kvadrat, eksponencijalna
|
|
| gama distribucija | X ~ Γ(α,λ) |
|
|
| hi-kvadrat distribucija | X ~ χ2(n) = Γ(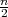 , ,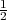 ) ) |
|
|
| eksponencijalna distribucija | X ~ Exp(λ) = Γ(1,λ) |
|
|
| očekivanje | E(X) = 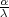 |
|
|
| varijanca | V ar(X) = 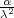 |
|
|
| hi-kvadrat Y ~ χ2(n) | Y = ∑
i=1n(X
i)2 |
|
|
| za | Xi ~ N(0,1) |
|
|
| |
STUDENTOVA ili t- DISTRIBUCIJA
|
|
| Studentova distribucija | X ~ t(n) |
|
|
| očekivanje | E(X) = 0 |
|
|
| varijanca | V ar(X) = 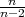 , za n > 2 , za n > 2 |
|
|
| Studentova razdioba T ~ t(n) | T = 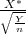 , , |
|
|
| ako je | X*~ N(0,1) i Y ~ χ2(n). |
|
|
| |
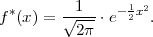
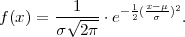
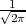
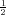
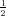
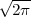
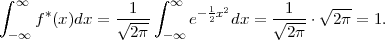
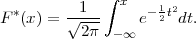
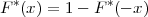
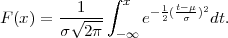
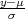
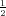
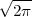
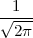
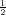
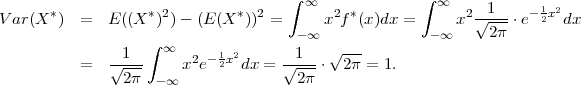
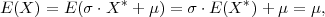
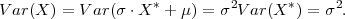
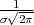
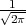
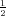
 ,
,