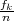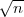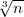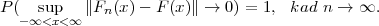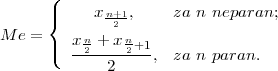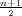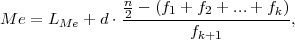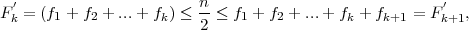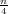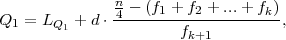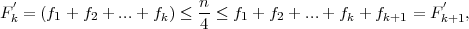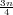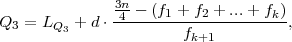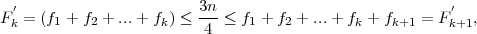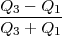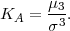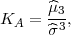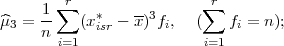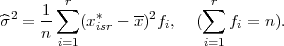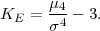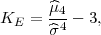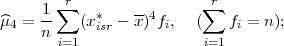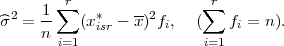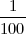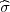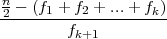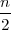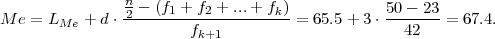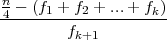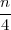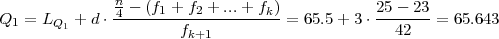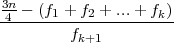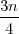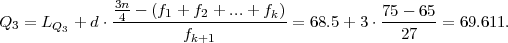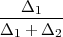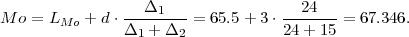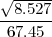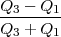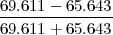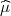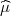Poglavlje 11
MATEMATIČKA STATISTIKA
Matematička statistika je znanstvena disciplina koja provjerava matematičke modele
slučajnog pokusa u realnosti. Proučava svojstva slučajnog uzoraka i donosi zaključke o
populaciji iz koje je uzet slučajni uzorak. Statističke metode daju zaključke s nekom
vjerojatnošću pa se temelje na teoriji vjerojatnosti.
Deskriptivna statistika bavi se uredivanjem prikupljenih, empirijskih podataka, njihovim
grafičkim prikazivanjem i opisivanjem pomoću numeričkih vrijednosti: prosjek,
standardna devijacija, korelacijski koeficijent,...
Induktivna statistika (Inferencijalna statistika )bavi se metodama koje se zasnivaju na
teoriji vjerojatnosti i koje omogućavaju da se donose zaključci o populaciji pomoću
uzoraka iz populacije.
Tri pravca u matematčkoj statistici (induktivnoj statististici) su:
teorija procjene,
teorija testiranja statističkih hipoteza,
teorija planiranja eksperimenata.
U teoriji procjene osvnut ćemo se na:
točkaste procjenitelje,
metodu max vjerojatnosti za odredivanje procjenitelja,tko želi znati više
intervale povjerenja za procjenitelje za parametre normalne razdiobe.
U teoriji testiranja osvnut ćemo se na:
test hipoteze o parametrima normalne razdiobe,
Teorija planiranja eksperimenta razvija metodu sekvencijalne analize, broj
promatranja je slučajan, pa se provjera statstičkih hipoteza ovom metodom
izvodi postepeno, u etapama. Hipoteza se može prihhvatiti, odbiti ili produžiti
eksperiment.
11.1 DESKRIPTIVNA STATISTIKA
Definicija 11.1 (POPULACIJA)
Populacija (osnovni skup, statistički skup) je skup svih elemenata od kojih
bismo mogli uzeti podatke o odredenim veličinama.
Populacija može biti konačna ili beskonačna.
PRIMJER 11.1
Populacija - sve obitelji u jednoj zgradi.
Veličine koje možemo razmatrati: broj djece, mjesečni dohodak..
Definicija 11.2 (STATISTIČKA VARIJABLA-OBILJEŽJE)
Statističko obilježje (vaijabla) je numeričko svojstvo elemenata statističkog
skupa.
Ako je skup vrijednosti R(X) statističkog obilježja diskretan onda za X kažemo da
je diskretno obilježje, a ako je R(X) ⊆ R kažemo da je kontinuirano obilježje.
Uzorak je podskup populacije koji uzimamo na unaprijed odreden način.
Definicija 11.3 (FREKVENCIJA, RELATIVNA FREKVENCIJA,
KUMULATIVNA RELATIVNA FREKVENCIJA, ARITMETIČKA SREDINA,
VARIJANCA, STANDARDNA DEVIJACIJA)
Neka je X statističko obilježje i neka se mjerenje ponovi n, konačno mnogo puta
(nezavisno) i dobije n statističkih podataka xi,i = 1,..,n. Slika R(X)={xk*,k =
1,..,r} sadrži r različitih statističkih podataka. Ako se xk* pojavi fk puta onda
kažemo da xk* pripada frekvencija fk i relativna frekvencija 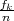 , za k = 1,..,r.
, za k = 1,..,r.
Vrijedi: ∑
k=1rfk = n, ∑
k=1r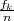 = 1.
= 1.
Za x ∈ R kažemo da ima kumulativnu relativnu frekvenciju Fn(x)=∑
k,xk≤x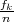 .
.
Aritmetička redina n statističkih podataka xi,i = 1,..,n:
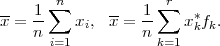
Varijanca n statističkih podataka xi,i = 1,..,n:
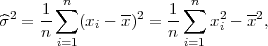
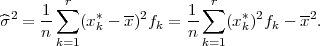
Standardna devijacija je 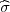 .
.
Statističke podatke koji se dobiju mjerenjem statističkog obilježja X možemo
prikazati:
tablično: tablicom frekvencija i tablicom relativnih frekvencija,
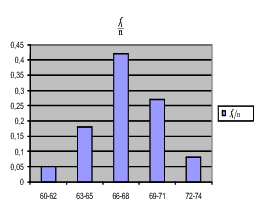
grafički: grafikonom frekvencija, relativnih frekvencija, kumulativnih frekvencija,
histogramom (nad dobivenim podacima xk* nacrtani su pravokutnici visine jednake
frekvenciji fkili relativnoj frekvenciji 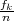 ),
),
poligonom (izlomljena linija koja spaja točke (xk*,fk)).
Ako je n veliki i skup vrijednosti ima veliki broj elemenata (posebno kod kontinuirane
slučajne varijable-statističkog obilježja) formiramo r razreda. Prilikom tabličnog i
grafičkog prikazivanja vrijednosti slučajnog uzorka na apscisu nanosimo r podintervala
(razreda), sa sredinama razreda xksr*, a na ordinatu sumu frekvencija fk elemenata iz
tog razreda.
Broj razreda r ponekad se računa po formulama: r = 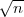 , r = 2
, r = 2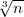 .
.
U praksi se koristi slijedeća shema za izbor broja razreda:

PRIMJER 11.2
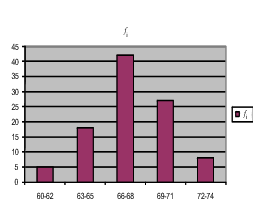
Mjerenjem kontinuirane slučajne varijable X= prosječne težine studenata
jednog turnusa na uzorku veličine 100 dobivena je vrijednost slučajnog uzorka
(x1,x2,...,x100) dana u tablici:
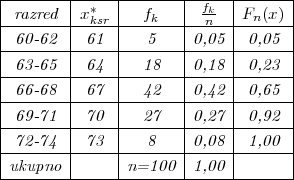
Relativne frekvencije odgovaraju pojmu statističke vjerojatnosti.
P(66 < X < 68) ≈ 0,42
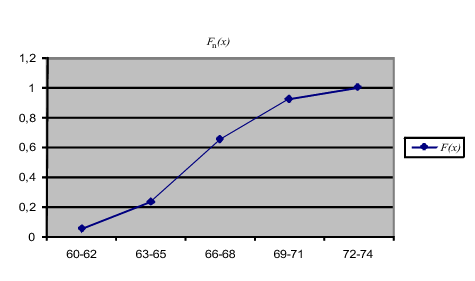
Definicija 11.4 (STATISTIČKA RAZDIOBA)
Statističko obilježje (slučajna varijabla) X sa skupom vrijednosti R(X) opisano
grafom relativnih frekvencija ili grafom kumulativnih relativnih frekvencija ima
statističku funkciju distribucije Fn(x). Slučajna varijabla X ima i teorijsku funkciju
distribucije F(x).
TEOREM 11.1 (GLIVENKO)
Ako su vrijednosti u uzorku slučajne varijable X (statističkog obilježja)
nezavisni, onda je
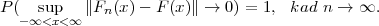
Kad je uzorak dovoljno velik, onda se s vjerojatnošću skoro 1 statistička razdioba
malo razlikuje od teorijske razdiobe.
Definicija 11.5 (Kvantil, medijan, prvi kvartil, treći kvartil)
Ako je F funkcija distribucije slučajne varijable X onda se rješenje jednadžbe
F(xp) = p zove kvantil reda p.
Medijan Me = x0.5; F(Me) = 0.5 tj. P(X ≤ Me) = 0.5
Prvi kvartil Q1 = x0.25; F(Q1) = 0.25 tj. P(X ≤ Q1) = 0.25
Drugi kvartil Q2 = x0.5 = Me
Treći kvartil Q3 = x0.75; F(Q3) = 0.75 tj. P(X ≤ Q3) = 0.75
PRIMJER 11.3 Računanje medijana statističkog obilježja X:
(A) Ako je niz statističkih podataka, vrijednosti nekog statističkog obilježja X
rastući x1 ≤ x2 ≤ ... ≤ xn, onda je
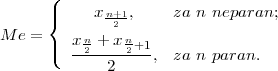
PRIMJER 11.4 Odredite medijan za zadani niz statističkih podataka
3 4 4 5 6 8 8 8 10, n=9, neparan.
Me = x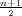 = x5 = 6.
= x5 = 6.
PRIMJER 11.5 Računanje medijana statističkog obilježja X:
(B) Ako su vrijednosti statističkog obilježja date u razredima s odgovarajućim
frekvencijama fi onda je
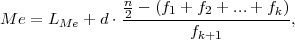
gdje je k izabran tako da je
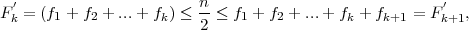
LMe je lijevi rub k + 1 razreda, d je širina razreda.
PRIMJER 11.6 Računanje prvog kvartila statističkog obilježja X:
(A) Ako je niz statističkih podataka, vrijednosti nekog statističkog obilježja X
rastući x1 ≤ x2 ≤ ... ≤ xn, onda je
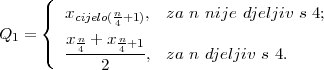
PRIMJER 11.7 Odredite prvi kvartil za niz statističkih podataka
3 4 4 5 6 8 8 8 10, n = 9, nije djeljiv s 4.
Q1 = xcijelo(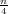 +1) = x3 = 4.
+1) = x3 = 4.
PRIMJER 11.8 Računanje prvog kvartila statističkog obilježja X:
(B) Ako su vrijednosti statističkog obilježja date u razredima s odgovarajućim
frekvencijama fi onda je
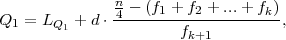
gdje je k izabran tako da je
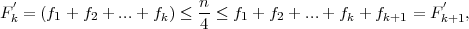
LQ1 je lijevi rub k + 1 razreda, d je širina razreda.
PRIMJER 11.9 Računanje trećeg kvartila:
(A) Ako je niz statističkih podataka, vrijednosti nekog statističkog obilježja X
rastući x1 ≤ x2 ≤ ... ≤ xn, onda je
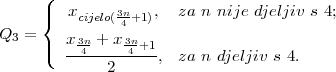
PRIMJER 11.10 Odredite treći kvartil niz statističkih podataka
3 4 4 5 6 8 8 8 10, n = 9, nije djeljiv s 4.
Q3 = xcijelo(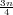 +1) = x7 = 8.
+1) = x7 = 8.
PRIMJER 11.11 Računanje trećeg kvartila:
(B) Ako su vrijednosti statističkog obilježja date u razredima s odgovarajućim
frekvencijama fi onda je
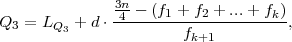
gdje je k izabran tako da je
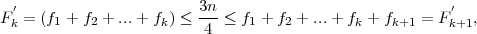
LQ3 je lijevi rub k + 1 razreda, d je širina razreda.
Definicija 11.6 (MOD)
Mod je vrijednost statističkog obilježja koja ima najveću frekvenciju. Može se
dogoditi da mod ne postoji ili da postoji više modova.
PRIMJER 11.12 Odredite mod niza statističkih podataka
3 4 4 5 6 8 8 8 10.
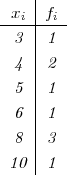
xi = 8 ima maksimalnu frekvenciju fi = 3, Mo = 8.
PRIMJER 11.13 Računanje moda:
Ako su vrijednosti statističkog obilježja date u razredima s odgovarajućim
frekvencijama fi onda je
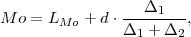
gdje je k izabran tako da je fk maksimalan, LMo je lijevi rub k -tog razreda, d je
širina razreda, Δ1 = fk - fk-1, Δ2 = fk - fk+1.
Definicija 11.7 (koeficijent varijacije)
Koeficijent varijacije je relativna mjera standardne devijacija i računa se na dva
načina
KV =  ⋅ 100 ili pomoću kvartila KV =
⋅ 100 ili pomoću kvartila KV = 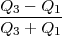 .
.
Definicija 11.8 (koeficijent asimetrije)
Koeficijent asimetrije za slučajnu varijablu X je broj KA koji karakterizira
simetriju razdiobe i definira se kao kvocijent trećeg centralnog momenta i kuba
standardne devijacije σ :
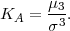
Definicija 11.9 Koeficijent asimetrije statističkog obilježja X, ako su vrijednosti
statističkog obilježja date kao niz xi* s frekvencijama fi, i = 1,...,r, definira se
kao
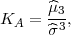
gdje je
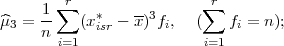
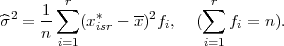
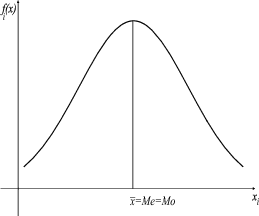
NAPOMENA 11.1 Ako je KA = 0 onda je razdioba frekvencija simetrična u
odnosu na pravac x = x onda se poklapaju x = Me = Mo. (Normalna razdioba
ima KA = 0)
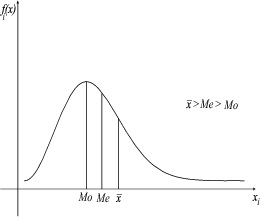
Ako je KA > 0 onda je razdioba frekvencija asimetrična u odnosu na pravac x = x,
asimetrija je pozitivna i vrijedi x > Me > Mo.
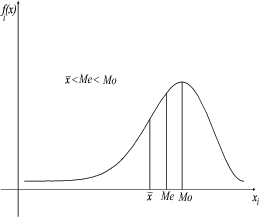
Ako je KA < 0 onda je razdioba frekvencija asimetrična u odnosu
na pravac x = x, asimetrija je negativna i vrijedi x < Me < Mo.
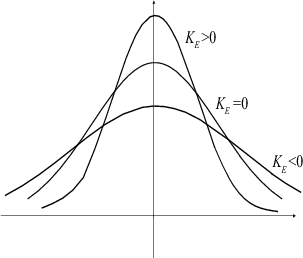
Definicija 11.10 koeficijent spljoštenosti (eksces)
Koeficijent spljoštenosti slučajne varijable X je broj KE koji karakterizira
zaobljenost razdiobe i definira se kao pomoću kvocijenta četvrtog centralnog
momenta i četvrte potencije standardne devijacije σ :
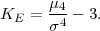
Definicija 11.11 Koeficijent spljoštenosti statističkog obilježja X, ako su
vrijednosti statističkog obilježja date kao niz xi* s frekvencijama fi, i = 1,...,r,
definira se kao
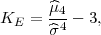
gdje je
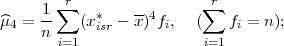
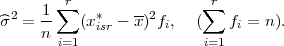
NAPOMENA 11.2 Ako je KE = 0 onda je razdioba frekvencija normalna
razdioba. (Normalna razdioba ima KE = 0)
Ako je KE > 0 onda je graf funkcije razdiobe frekvencija uži od grafa normalne
razdiobe (spljoštenost je manja).
Ako je KE < 0 onda je graf funkcije razdioba frekvencija širi od normalne razdiobe
(spljoštenost je veća).
PRIMJER 11.14 Mjerenjem kontinuirane slučajne varijable X= prosječne
težine studenata jednog turnusa na uzorku veličine 100 dobivena je vrijednost
slučajnog uzorka (x1,x2,...,x100) dana u tablici:
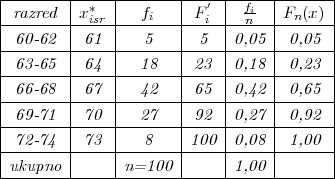
Odrediti očekivanje, varjancu, standardnu devijaciju, mod, medijan, prvi kvartil,
treći kvartil, koeficijent varijacije, koeficijent asimetrije, koeficijent spljoštenosti.
NAPOMENA: Razredi su u tablici dati smbolično npr. razred 60 - 62 je razred
59.5 - 62.5 tako da je širina razreda d = 3.
Rješenje:
očekivanje x = 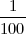 ∑
i=15x
isr*f
i = 67.45
∑
i=15x
isr*f
i = 67.45
varijanca 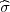 2 =
2 =  ∑
i=1r(x
isr*-x)2f
i = 8.527
∑
i=1r(x
isr*-x)2f
i = 8.527
medijan Me = LMe + d ⋅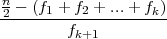 , gdje je k + 1 = 3 izabran tako da je
Fk′
= f1 + f2 = 23 ≤
, gdje je k + 1 = 3 izabran tako da je
Fk′
= f1 + f2 = 23 ≤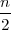 = 50 ≤ f1 + f2 + f3 = 65 = Fk+1′
,
= 50 ≤ f1 + f2 + f3 = 65 = Fk+1′
,
LMe = 65.5 je lijevi rub k + 1 = 3. razreda, d = 3 je širina razreda.
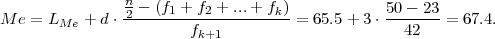
prvi kvartil Q1 = LQ1 + d ⋅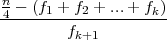 , gdje je k + 1 = 3 izabran tako da
je Fk′
= f1 + f2 = 23 ≤
, gdje je k + 1 = 3 izabran tako da
je Fk′
= f1 + f2 = 23 ≤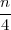 = 25 ≤ f1 + f2 + f3 = 65 = Fk+1′
,
= 25 ≤ f1 + f2 + f3 = 65 = Fk+1′
,
LQ1 = 65.5 je lijevi rub k + 1 = 3. razreda, d = 3 je širina razreda.
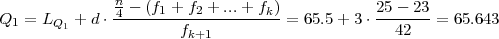
treći kvartil Q3 = LQ3 + d ⋅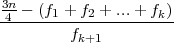 , gdje je k + 1 = 4 izabran tako da
je Fk′
= f1 + f2 + f3 = 65 ≤
, gdje je k + 1 = 4 izabran tako da
je Fk′
= f1 + f2 + f3 = 65 ≤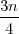 = 75 ≤ f1 + f2 + f + f4 = 92 = Fk+1′
,
= 75 ≤ f1 + f2 + f + f4 = 92 = Fk+1′
,
LQ3 = 68.5 je lijevi rub k + 1 = 4. razreda, d = 3 je širina razreda.
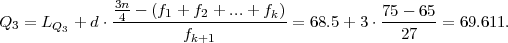
mod Mo = LMo + d ⋅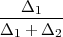 , gdje je k = 3 izabran tako da je fk = 42
maksimalan, LMo = 65.5 je lijevi rub k = 3. razreda, d = 3 je širina razreda,
Δ1 = fk - fk-1 = f3 - f2 = 42 - 18, Δ2 = fk - fk+1 = f3 - f4 = 42 - 27.
, gdje je k = 3 izabran tako da je fk = 42
maksimalan, LMo = 65.5 je lijevi rub k = 3. razreda, d = 3 je širina razreda,
Δ1 = fk - fk-1 = f3 - f2 = 42 - 18, Δ2 = fk - fk+1 = f3 - f4 = 42 - 27.
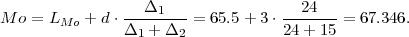
koeficijent varijacije KV =  ⋅ 100% =
⋅ 100% = 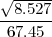 ⋅ 100% = 4.32%
⋅ 100% = 4.32%
KV = 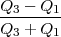 =
= 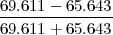 = 2.9337 × 10-2
= 2.9337 × 10-2
koeficijet asimetrije i spljoštenosti 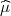 3 =
3 =  ∑
i=1r(x
isr*-x)3f
i = -2.293
∑
i=1r(x
isr*-x)3f
i = -2.293
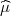 4 =
4 =  ∑
i=1r(x
isr*-x)4f
i = 199.37
∑
i=1r(x
isr*-x)4f
i = 199.37
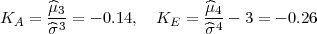
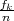 , za k = 1,..,r.
, za k = 1,..,r.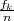 = 1.
= 1.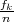 .
.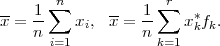
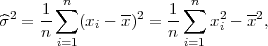
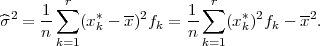
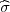 .
.